欧拉线与九点圆

三角形的五心

定义与基本性质

定义1：内心

三角形三条内角平分线的交点称为内心，记作 $I$。内心是内切圆的圆心，到三边的距离相等。

证明内心存在性：

设 $\triangle ABC$ 中，$\angle A$ 的平分线交 $BC$ 于 $D$，$\angle B$ 的平分线交 $AC$ 于 $E$。设角平分线 $AD$ 和 $BE$ 交于点 $I$。过 $I$ 作 $BC,CA,AB$ 的垂线，垂足分别为 $P,Q,R$。

• 因为 $I$ 在 $\angle A$ 的平分线上，$IP = IQ$

• 因为 $I$ 在 $\angle B$ 的平分线上，$IP = IR$

• 故 $IP = IQ = IR$

因此 $I$ 到三边距离相等，$CI$ 也是 $\angle C$ 的平分线，三条角平分线交于一点。

定义2：外心

三角形三条边的垂直平分线的交点称为外心，记作 $O$。外心是外接圆的圆心，到三个顶点的距离相等。

证明外心存在性：

设 $AB$ 的垂直平分线为 $l_{1}$，$BC$ 的垂直平分线为 $l_{2}$，它们交于点 $O$。对于 $l_{1}$ 上任一点，到 $A,B$ 距离相等；对于 $l_{2}$ 上任一点，到 $B,C$ 距离相等。故 $O$ 满足：

\[OA = OB = OC\]

因此 $O$ 也在 $AC$ 的垂直平分线上，三条中垂线交于一点。

定义3：重心

三角形三条中线的交点称为重心，记作 $G$。重心将每条中线分为 2:1 两部分（靠近顶点的部分较长）。

证明重心存在性及性质：

使用向量法。设 $\triangle ABC$ 的顶点坐标为 $A,B,C$。边 $BC$ 的中点为 $M_{a} = \frac{B + C}{2}$。中线 $AM_{a}$ 上的点可表示为：

\[P = A + t\left( M_{a} - A \right) = A + t\left( \frac{B + C}{2} - A \right) = (1 - t)A + \frac{t}{2}B + \frac{t}{2}C\]

类似地，中线 $BM_{b}$ 上的点可表示为：$Q = (1 - s)B + \frac{s}{2}A + \frac{s}{2}C$。

若两中线交于一点，则：

\[(1 - t)A + \frac{t}{2}B + \frac{t}{2}C = \frac{s}{2}A + (1 - s)B + \frac{s}{2}C\]

比较系数得：$1 - t = \frac{s}{2},\frac{t}{2} = 1 - s$，解得 $t = s = \frac{2}{3}$。

故重心坐标为：

\[G = \frac{A + B + C}{3}\]

重心到顶点的距离是重心到对边中点距离的2倍。

定义4：垂心

三角形三条高的交点称为垂心，记作 $H$。

证明垂心存在性：

角元赛瓦定理

定义5：旁心

三角形一个内角的角平分线与其余两个内角的外角平分线交于一点，称为对该顶点的旁心，记作 $I$、对顶点 $B$ 的旁心记作 $I_{b}$，对顶点 $C$ 的旁心记作 $I_{c}$。

欧拉线

欧拉线的定义

定义6：欧拉线

在任意非正三角形中，垂心 $H$、重心 $G$、外心 $O$ 三点共线，这条直线称为欧拉线。

欧拉线定理的证明

定理3：欧拉线定理

三角形的垂心 $H$、重心 $G$、外心 $O$ 三点共线，且：

\[HG = 2 \cdot OG\]

即重心 $G$ 分线段 $OH$ 为 $2:1$（靠近垂心的部分较长）。

证明方法一：纯几何证明

设 $\triangle ABC$ 的垂心、重心、外心分别为 $H,G,O$。

延长 $BO$ 交外接圆于点 $D$，连接 $AH,AD,CD,CH$。

因为 $BD$ 是外接圆的直径，所以：

\[\angle BCD = 90^\circ,\quad\angle BAD = 90^\circ\]

即 $CD \perp BC$，$AD \perp AB$。

又因为 $H$ 是垂心，所以：

\[AH \perp BC,\quad CH \perp AB\]

因此：

\[CD \parallel AH,\quad AD \parallel CH\]

所以 $ADCH$ 是平行四边形，因此：

\[AH = DC\]

设 $M_{a}$ 是 $BC$ 的中点。因为 $O,M_{a}$ 分别是 $BD,BC$ 的中点，所以 $OM_{a}$ 是 $\triangle DBC$ 的中位线，因此：

\[OM_{a} \parallel DC,\quad OM_{a} = \frac{1}{2}DC = \frac{1}{2}AH\]

连接 $AM_{a}$（这是中线）。设 $OH$ 交 $AM_{a}$ 于点 $G’$。

在 $\triangle AHG’$ 和 $\triangle M_{a}OG’$ 中：

\[AH \parallel OM_{a},\quad\text{ 且 }\quad AH = 2 \cdot OM_{a}\]

因此 $\triangle AHG’ \sim \triangle M_{a}OG’$，相似比为 $2:1$。

所以：

\[AG' = 2 \cdot G' M_{a}\]

这说明 $G’$ 是中线 $AM_{a}$ 上的一个三等分点（距顶点 $A$ 较近）。

由重心的定义，重心 $G$ 也是中线 $AM_{a}$ 上距顶点较近的三等分点，因此 $G’ = G$。

所以 $O,G,H$ 三点共线，且 $HG = 2 \cdot OG$。Q.E.D.

证明方法二：向量证明

使用坐标或向量方法更加简洁。设 $\triangle ABC$ 的顶点为 $A,B,C$。

外心 $O$ 满足：

\[|OA| = |OB| = |OC|\]

设 $O$ 为原点，则：

\[|A|^{2} = |B|^{2} = |C|^{2}\]

重心为：

\[G = \frac{A + B + C}{3}\]

垂心 $H$ 满足 $\vec{AH} \perp \vec{BC}$，$\vec{BH} \perp \vec{AC}$，$\vec{CH} \perp \vec{AB}$。

垂心 $H$ 满足两条高线的垂直条件：

1. $(H - A) \cdot (B - C) = 0$

2. $(H - B) \cdot (C - A) = 0$

展开得

\[H \cdot (B - C) = A \cdot (B - C),\quad H \cdot (C - A) = B \cdot (C - A).\]

将假设 $H = A + B + C$ 代入左式：

\[(A + B + C) \cdot (B - C) = A \cdot B - A \cdot C + |B|^{2} - |C|^{2} = A \cdot B - A \cdot C\]

因为 $\vert B\vert ^{2} = \vert C\vert ^{2}$

因此：

\[G = \frac{H}{3} = \frac{1}{3}(A + B + C)\]

这说明 $O,G,H$ 共线（都在从原点 $O$ 出发的方向上），且：

\[\vec{OG} = \frac{1}{3}\vec{OH}\]

即 $G$ 在 $OH$ 上，且 $OG:GH = 1:2$，或 $HG = 2 \cdot OG$。Q.E.D.

九点圆

九点圆的定义

定义7：九点圆

对于任意三角形，以下九个点共圆：

1. 三边的中点：$M_{a},M_{b},M_{c}$

2. 三条高的垂足：$D,E,F$

3. 从各顶点到垂心的线段中点：$X,Y,Z$

这个圆称为九点圆，也称欧拉圆或费尔巴哈圆。

九点圆的证明

定理1：九点圆定理

三角形的九点（三边中点、三高垂足、垂心到顶点的中点）共圆。

证明：

STEP1：构造矩形

设 $\triangle ABC$ 的外心、垂心分别为 $O,H$。设三边中点为 $M_{a},M_{b},M_{c}$，垂心到顶点的中点为 $X,Y,Z$（即 $X$ 是 $AH$ 中点，$Y$ 是 $BH$ 中点，$Z$ 是 $CH$ 中点）。

由欧拉线性质，有：

\[OM_{c} \parallel CH,\quad OM_{c} = \frac{1}{2}CH\]

因为 $M_{a}$ 是 $BC$ 的中点，$Y$ 是 $BH$ 的中点，由三角形中位线定理：

\[M_{a}Y \parallel CH,\quad M_{a}Y = \frac{1}{2}CH\]

同理，$M_{b}$ 是 $AC$ 的中点，$X$ 是 $AH$ 的中点：

\[M_{b}X \parallel CH,\quad M_{b}X = \frac{1}{2}CH\]

因此：

\[M_{b}X \parallel M_{a}Y \parallel M_{c}O,\quad M_{b}X = M_{a}Y = M_{c}O\]

再由三角形中位线定理：

\[M_{a}M_{b} \parallel XY \parallel AB,\quad M_{a}M_{b} = XY = \frac{1}{2}AB\]

外心 $O$ 到中点 $M_{c}$ 的连线是 $AB$ 的中垂线，故 $OM_{c} \perp AB$。因此：

\[M_{a}M_{b} \perp M_{a}Y\]

所以四边形 $M_{a}M_{b}XY$ 是矩形。

STEP2：证明六点共圆

由矩形性质，$M_{a},M_{b},X,Y$ 四点共圆，且 $M_{b}Y$ 和 $M_{a}X$ 是该圆的直径。

同理可证，四边形 $XM_{c}M_{a}Z$ 也是矩形，因此 $X,M_{c},M_{a},Z$ 四点共圆，且 $XM_{a}$ 和 $M_{c}Z$ 是该圆的直径。

因为这两个圆都以 $XM_{a}$ 为直径，所以它们是同一个圆。因此：

\[M_{a},M_{b},M_{c},X,Y,Z\text{ 六点共圆 }\]

STEP3：证明垂足也在圆上

设 $D,E,F$ 分别是从 $A,B,C$ 向对边作高的垂足。

因为 $CF$ 是三角形的高，$\angle CFB = 90^\circ$。而 $M_{c}$ 是 $AB$ 的中点，$Z$ 是 $CH$ 的中点。在直角三角形中，斜边中点到直角顶点的距离等于斜边的一半。

考虑 $\angle M_{c}FZ$：因为 $M_{c}Z$ 是上述圆的直径，而 $\angle CFB = 90^\circ$，根据圆周角定理，可以证明 $F$ 在以 $M_{c}Z$ 为直径的圆上。

同理，$D,E$ 也在这个圆上。

因此，九点 $M_{a},M_{b},M_{c},D,E,F,X,Y,Z$ 共圆。Q.E.D.

九点圆的性质

定理2：九点圆的半径

九点圆的半径等于外接圆半径的一半。

证明：

由前面的证明，$M_{c}Z$ 是九点圆的直径。

因为 $OM_{c} \parallel CH$ 且 $OM_{c} = \frac{1}{2}CH = ZH = CZ$（$Z$ 是 $CH$ 的中点），所以：

\[OM_{c} \parallel ZH,\quad OM_{c} = ZH\]

因此四边形 $OM_{c}HZ$ 是平行四边形，对角线 $M_{c}Z$ 和 $OH$ 互相平分。

又因为 $OM_{c} = CZ$ 且 $OM_{c} \parallel CZ$，所以 $OM_{c}CZ$ 也是平行四边形，因此：

\[OC = M_{c}Z\]

因为 $O$ 是外心，$OC$ 是外接圆的半径 $R$。$M_{c}Z$ 是九点圆的直径，因此九点圆的半径为：

\[r = \frac{M_{c}Z}{2} = \frac{OC}{2} = \frac{R}{2}\]

Q.E.D.

九点圆圆心在欧拉线上

定理陈述

定理4：九点圆圆心的位置

九点圆的圆心 $N$ 位于欧拉线上，且是垂心 $H$ 与外心 $O$ 的中点。

证明

由前面九点圆的证明，我们知道 $M_{c}Z$ 是九点圆的直径（其中 $M_{c}$ 是 $AB$ 的中点，$Z$ 是 $CH$ 的中点）。

因此九点圆的圆心 $N$ 是 $M_{c}Z$ 的中点。

我们已经证明了四边形 $OM_{c}HZ$ 是平行四边形（因为 $OM_{c} \parallel ZH$ 且 $OM_{c} = ZH$）。

平行四边形的对角线互相平分，因此 $M_{c}Z$ 和 $OH$ 的交点就是它们各自的中点。

所以 $N$ 既是 $M_{c}Z$ 的中点，也是 $OH$ 的中点。

因为 $O$ 和 $H$ 都在欧拉线上，所以 $OH$ 的中点 $N$ 也在欧拉线上。

综上所述，九点圆圆心 $N$ 是 $O$ 和 $H$ 的中点，位于欧拉线上。

我们可以进一步得出欧拉线上四点的位置关系：

\[O,N,G,H\text{ 共线 }\]

且：

\[ON:NG:GH = 1:1:2\]

或者说 $ON = NG = \frac{1}{2}GH$。Q.E.D.

典型例题

设 $O$，$H$ 分别是 $\triangle ABC$ 的外心和垂心，$E$，$F$ 分别是边 $AC$，$AB$ 的中点，已知 $HF\perp MF$，$HE\perp NE$，$M$ 在 $CA$ 直线上，$N$ 在 $AB$ 直线上. 证明：$HO\perp MN$.

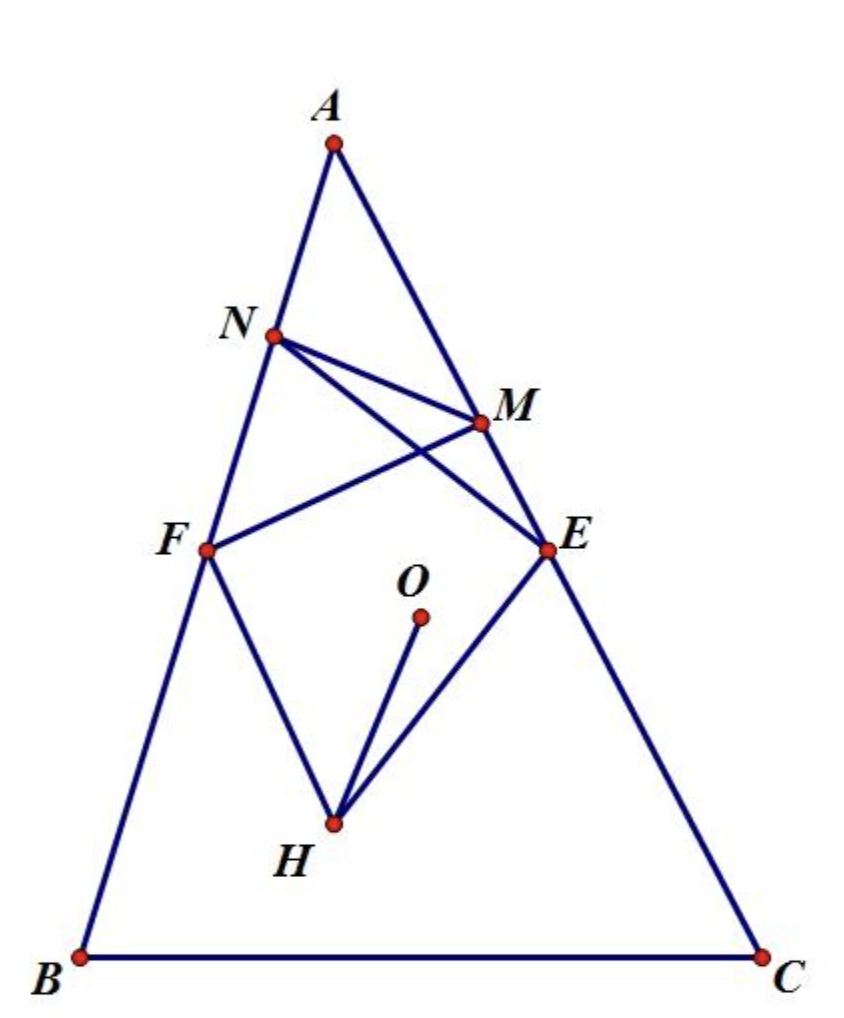
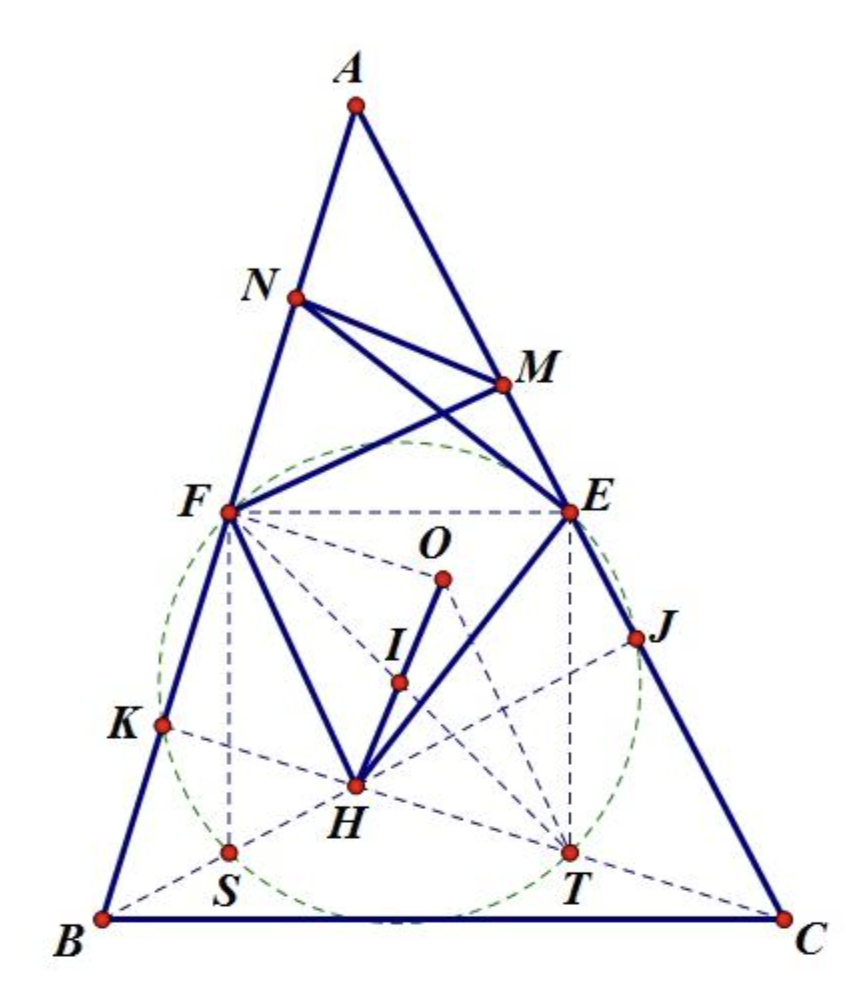
作 $\triangle ABC$ 的九点圆，圆心为 $OH$ 中点 $I$

由九点圆性质，四边形 $EFST$ 为矩形

$\therefore$ $SF\perp FE$ $HF\perp MF$ $\therefore\angle SFH = \angle EFM$

$\therefore$ $E, F, S, T$ 共圆（九点圆） $\therefore\angle MEF = \angle HSF$

$\therefore$ $\triangle FSH \sim \triangle FEM$ $FH/FM = FS/FE$

同理 $\triangle EHT \sim \triangle ENF$ $HT/NF = ET/EF$

$\therefore$ $FT$ 过圆心 $I$ $I$ 为 $FT \wedge OH$ 中点

故四边形 $OFHT$ 为平行四边形

$\therefore$ $OF = HT$ 注意到 $FS = ET \Rightarrow FH/FM = OF/NF$

$\therefore$ $OF\perp NF$ $HF\perp FM$ $\therefore\angle OFH = \angle NFM$

故 $\triangle OFH \sim \triangle NFM$ $OF\perp NF$ $FH\perp FM$

$\therefore$ $OH\perp NM$

Q.E.D.